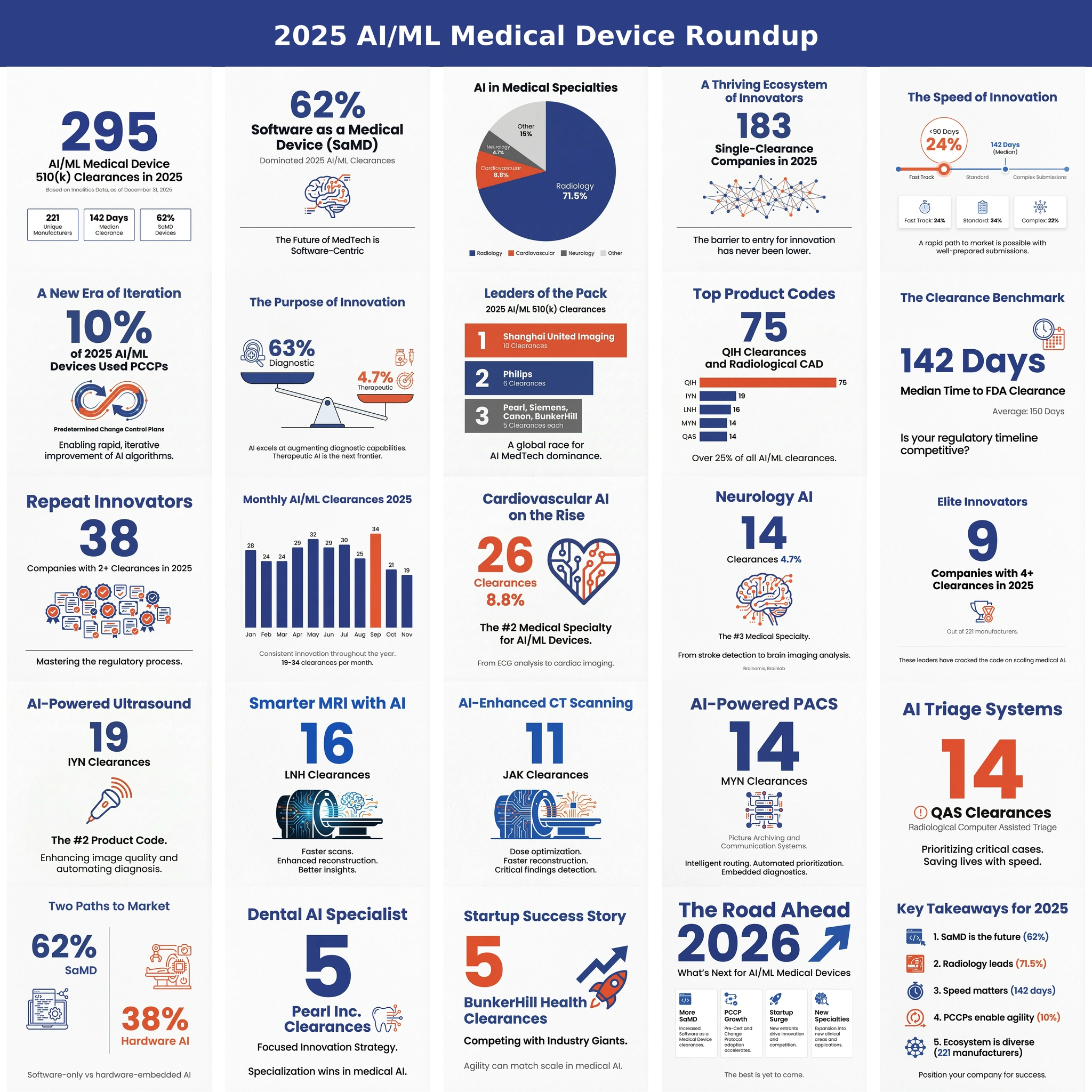
Introduction 🔗
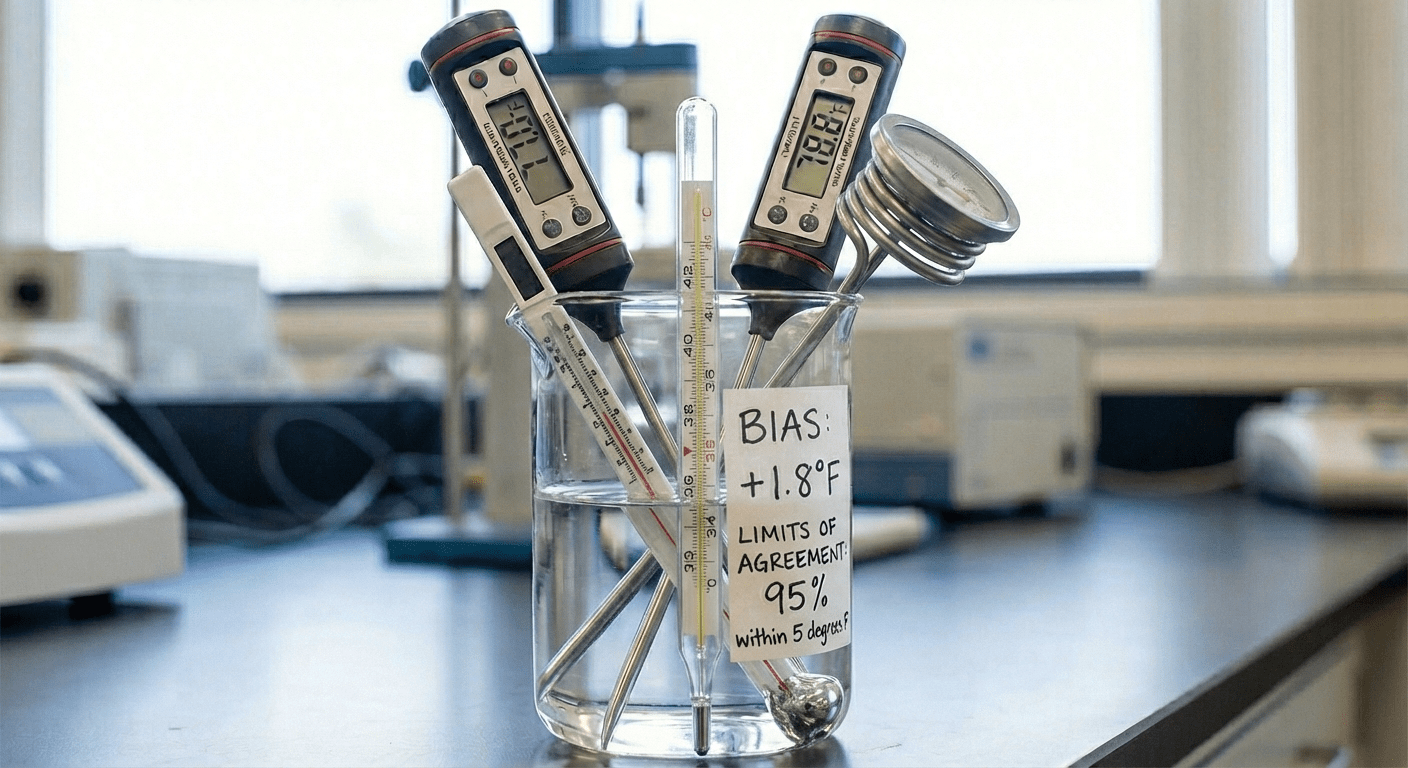
Evaluating agreement between an AI/ML medical device and a clinical reference standard is essential for regulatory acceptance. While metrics like AUC, Sensitivity/Specificity and Dice scores describe discriminative performance, they do not address whether two measurement methods can be used interchangeably. High discriminative performance can coexist with unacceptable systematic bias or clinically meaningful measurement deviation. Bland-Altman analysis is the FDA-preferred method to quantify agreement, bias, and limits of acceptable error.
What is Bland-Altman Analysis? 🔗
Bland–Altman analysis is a statistical method used to evaluate the agreement between two quantitative measurement techniques, such as assessing whether measurements obtained from an AI-enabled medical device can be considered interchangeable with those from an established clinical reference standard. In the context of clinical validation, it is essential to demonstrate that a new method is both reliable and reproducible. Because every measurement contains some degree of error and neither method can be assumed perfectly correct, Bland–Altman analysis provides a principled way to quantify the extent of disagreement and determine whether it is clinically acceptable.
The approach is typically implemented through the Bland–Altman plot. Bland–Altman plots, also known as difference plots, are a graphical tool for comparing two measurement techniques and assessing the agreement between paired measurements. The plot displays the difference between two measurements on the y-axis and the average of the two measurements on the x-axis. In essence, a Bland–Altman plot is a scatter plot in which the differences between measurements are plotted against their means, enabling visualization of agreement patterns and identification of potential systematic bias.
Why is a Bland–Altman Plot Required? 🔗
The fundamental objective in evaluating two measurement methods is to determine whether they are sufficiently comparable that one may replace the other with acceptable accuracy for the intended clinical application. Traditional statistical approaches such as correlation coefficients or linear regression are often misused to evaluate agreement. However, high correlation does not imply good agreement. Correlation measures the strength of association, not agreement. Two methods can correlate strongly while still exhibiting clinically unacceptable bias or variability.
For example, if one device systematically overestimates all values by a fixed amount, the correlation between the methods may be nearly 1.0, even though the measurements cannot be used interchangeably. Therefore, correlation and regression should not be used as primary tools for method comparison, as emphasized by Bland and Altman.
Bland–Altman analysis addresses these limitations by directly evaluating bias (systematic difference) and random error (dispersion of differences). The method compares paired measurements by plotting the difference between two methods (M1 − M2) against their average ((M1 + M2)/2). Reference lines provide clinically interpretable context:
- Horizontal line at zero difference (no bias)
- Mean difference (bias) line
- Limits of Agreement (LOA): Bias ± 1.96 × SD, representing the 95% confidence interval in which ~95% of differences are expected if normally distributed
This approach allows assessment of:
- Magnitude of disagreement
- Direction of systematic error
- Presence of proportional bias (difference changing with magnitude)
- Outliers
Illustrative Example 🔗
Consider the example from Altman and Bland (1983) comparing two systolic blood pressure measurement methods. The dataset includes 25 paired observations. The initial scatter plot of Method 1 vs. Method 2 suggests high agreement.

The below Bland–Altman plot assesses how well two measurement methods agree by plotting the difference between the methods (M1–M2) against their average. The central horizontal line shows the mean difference (bias), indicating whether one method tends to give higher values. The limits of agreement, shown as dashed lines at the mean difference ±1.96 SD, indicate the range in which 95% of differences fall and are used to judge whether the methods are interchangeable. In this plot, the mean difference is above zero showing that M1 tends to read higher than M2 and the limits of agreement are wide, with differences increasing at higher blood pressure levels, suggesting poor agreement and possible proportional bias between the two methods.

Although the scatter plot of the two measurement methods suggested high agreement because the points fell close to the line of equality. A Bland–Altman plot reveals a more realistic picture of their agreement. Scatter plots can hide important differences, especially when both methods are strongly correlated, which is common in biological measurements. The Bland–Altman plot shows that despite the high correlation, the actual differences between the two methods are large and increase with higher blood pressure values, indicating systematic bias and poor interchangeability. This contrast illustrates why correlation alone is insufficient for assessing agreement and why Bland–Altman analysis is the preferred method for evaluating whether two measurement methods can truly be used interchangeably.
Methodology 🔗
Bland and Altman introduced the Limits of Agreement (LOA) framework to quantify the expected variability between two methods. The idea is to examine how much two measurements differ for the same subject and whether that level of disagreement is acceptable.
Key Calculations 🔗
- Bias (mean difference)
Bias = mean(A − B)
- Limits of Agreement (LOA)
LOA = Bias ± 1.96 × SD
Where:
- Bias indicates systematic difference between methods
- SD is the standard deviation of the paired differences
- LOA represents the 95% confidence interval where approximately 95% of differences are expected to fall
Plot design 🔗
- X-axis: mean of the two measurements (A + B) / 2
- Y-axis: difference between measurements (A − B)
How to Interpret the Plot 🔗
A well-behaved comparison typically shows:
- Around 95% of points falling within the LOA
- No systematic trend or proportional bias as measurement magnitude increases
- Random scatter without clear patterns or shape change
How can a Bland-Altman Plot be used? 🔗
The Bland-Altman plot can be used to Evaluate agreement, Identify any systematic bias and find outliers in the data.
Evaluate agreement 🔗
The primary use of the Bland-Altman plot is to determine if two methods agree well enough to be used interchangeably in a clinical or practical setting. The Limits of Agreement (LOA) define the expected range for 95% of individual differences. If the LOA are narrow enough to be clinically irrelevant, the methods are interchangeable and if the LOA are too wide, the random error between the methods is too great for them to be considered equivalent, even if the average bias is zero.
Identify Systematic and Proportional Bias 🔗
The plot helps diagnose consistent errors present in one measurement technique compared to the other.
- Systematic Bias: Indicated by the mean difference line being consistently above or below zero. This suggests that one method always measures higher or lower than the other on average.
- Proportional Bias (Trends): This is identified visually if the data points form a funnel shape or have a clear slope. Proportional bias means the magnitude of the difference changes as the magnitude of the measurement changes (e.g., the methods agree for low values but not for high values).
Find outliers in the data 🔗
Points that fall outside the 95% limits of agreement are considered potential outliers. It is important to investigate these specific measurements to understand if there were errors in the data collection or if the individual had unique characteristics affecting the measurements.
Example plot: 🔗

Example of when Bland–Altman matters: two glucose methods can track together yet still disagree by clinically meaningful amounts.
Simple plot 🔗
An example of a Bland-Altman plot is to compare the measurement of blood sugar using two different measuring systems. In this case the x-axis is the mean of the two measurements and the y-axis is the difference between the two measuring systems. The plot would show the agreement or disagreement between the two measurement techniques.

Examples Demonstrating Different Agreement Scenarios 🔗
The image illustrates four different Bland–Altman plots demonstrating how patterns in measurement differences reveal agreement (or lack thereof) between two measurement methods or two observers. In all plots, the x-axis represents the mean of the paired measurements, and the y-axis represents the difference between the methods (Test2 − Test1). The solid horizontal line shows the mean bias, and the dashed lines indicate the limits of agreement (LOA).
Example A — Good Agreement, Minimal Bias, Narrow LOA 🔗
- The mean difference is close to zero, indicating no systematic bias.
- Most points lie tightly within the limits of agreement.
- Suggests that the two methods can be used interchangeably for clinical or measurement purposes.
Example B — Systematic Bias, Narrow LOA 🔗
- Points cluster close together with narrow LOA, showing high precision.
- However, the bias is significantly above zero, meaning one method consistently measures higher than the other.
- Strong repeatability, but measurements are not interchangeable without bias correction.
Example C — Minimal Bias, Wide LOA 🔗
- Mean bias is near zero, indicating little systematic shift.
- The spread of differences is large (broad LOA), meaning high variability between measurements.
- Agreement is poor due to lack of precision, even though average levels match.
Example D — Minimal Bias, Very Wide LOA (Worst Case) 🔗
- Very low bias but extremely broad LOA, indicating major inconsistency.
- Measurements are unreliable and not clinically acceptable.
- Demonstrates how low bias alone does not guarantee agreement.

Examples Demonstrating Different Biases 🔗
- Case of an absolute systematic error On average, TEST2 measures about 5.3 units lower than TEST1 showing the systematic bias of 5.3. However, the difference does not appear to depend on measurement size. Agreement may be acceptable depending on the clinical tolerance for ±13.5 units. If accuracy within that range is acceptable, the methods may be interchangeable.
- Case of a proportional error Agreement is poor. The amount of disagreement depends on measurement magnitude. These methods should not be used interchangeably without applying correction.
- Case where the variation of at least one method depends strongly on the magnitude of measurements The variability of the difference depends on the magnitude of the measurement, meaning agreement worsens as values increase. Even though the bias is small, the variation is not constant, which violates one of the assumptions for standard Bland–Altman analysis.
Example Code 🔗
- Using python function
import numpy as np
import matplotlib.pyplot as plt
def bland_altman_analysis(method_a, method_b, plot=True):
"""
Perform Bland–Altman agreement analysis between two measurement methods.
Parameters
----------
method_a : array-like
Measurements from method A (e.g., AI model).
method_b : array-like
Measurements from method B (e.g., clinical reference).
plot : bool, optional
If True, generates the Bland–Altman plot.
Returns
-------
results : dict
Dictionary containing bias, SD, and LOA bounds.
"""
method_a = np.array(method_a)
method_b = np.array(method_b)
# Pairwise differences and means
diff = method_a - method_b
mean_vals = (method_a + method_b) / 2
# Core Bland–Altman statistics
bias = np.mean(diff)
sd = np.std(diff, ddof=1)
loa_low = bias - 1.96 * sd
loa_high = bias + 1.96 * sd
results = {
"bias": bias,
"sd": sd,
"loa_low": loa_low,
"loa_high": loa_high
}
# Bland–Altman Plot
if plot:
plt.figure(figsize=(8, 6))
plt.scatter(mean_vals, diff, alpha=0.5)
plt.axhline(bias, linestyle='--', label="Bias")
plt.axhline(loa_low, linestyle='--', label="Lower LOA")
plt.axhline(loa_high, linestyle='--', label="Upper LOA")
plt.xlabel("Mean of Measurements")
plt.ylabel("Difference (A - B)")
plt.title("Bland–Altman Plot")
plt.grid(alpha=0.3)
plt.legend()
plt.show()
return results
# Generate example simulated data
np.random.seed(42)
true_values = np.random.normal(100, 10, 200)
method_a = true_values
method_b = true_values + np.random.normal(1.5, 4, 200)
results = bland_altman_analysis(method_a, method_b, plot=True)
print(results)
- Using Pingouin library
import numpy as np
import pingouin as pg
import matplotlib.pyplot as plt
# Generate example simulated data
np.random.seed(42)
true_values = np.random.normal(100, 10, 200)
method_a = true_values
method_b = true_values + np.random.normal(1.5, 4, 200)
pg.plot_blandaltman(method_a, method_b)
plt.title("Bland–Altman Plot")
plt.show()
Pitfalls in Bland-Altman analysis 🔗
One of the critical problems in the Bland-Altman analysis is the need to meet the assumption of normal distribution. The continuous measurement variables need not to be normally distributed, but their differences should. If the assumption of normal distribution is not met, data may be logarithmically transformed.
Another problem arises from the sample size. Studies comparing methods of measurements should be adequately sized to conclude that the effects are universally valid. If the sample size is not adequate, it is possible to find a low mean bias and reduced limits of agreement by comparing two methods. Such methods cannot be recommended for general use without verification of the results of other studies. To calculate sample size, maximum allowed difference derived from other studies should be provided.
An other problem in the Bland-Altman analysis is repeated measure designs. The Bland-Altman analysis is not an appropriate method to compare repeated measurements. However, it can be performed by adding a random effects model to the analysis. In addition, some statistical softwares allow to perform analysis for repeated designs using Bland-Altman method.
Frequently Asked Questions 🔗
Conclusion 🔗
If your device outputs a number, FDA is going to ask the obvious question: how far off is it, and when does that matter clinically?
Bland-Altman is the fastest way to turn that into a clearance-ready story. It connects your measurement performance to a pre-defined clinical tolerance, and it supports the claims, labeling, and study design you need for a credible 510(k) or De Novo package.
Done right, this is not "stats for stats' sake." It is risk reduction. Fewer avoidable review questions. Fewer late changes to claims. Less chance you run a study that cannot support the business outcome: FDA clearance.
Want to de-risk FDA clearance for a quantitative AI/ML device? Our FDA pre-sub service helps you set clinically acceptable LOA up front, pressure-test claims, and lock the validation plan before you spend real money on the pivotal study.